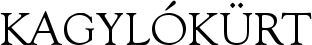A számok bűvöletében
A számok bűvöletében
„Nem a győzelem a fontos, hanem a részvétel” – tartja Pierre de Coubertin báró híres mondása. Az újkori ötkarikás játékok kimondott célja az volt, „hogy egyrészt a testi nevelés érdekében, másrészt a nemzetközi érintkezés előmozdítására az ókori Olympiadok időrendjének mintájára négyévenként nemzetközi versenyek rendeztessenek, s ezekre a világ minden kulturnemzete meghivassék”.
Így 2672 évvel az első ókori Olympiai játékok után 1896-ban, Athénben megrendezték az első újkori versenyt. Mára a részvétel helyébe a kíméletlen versengés lépett, amit a játékok jelmondata, a Citius, altius, fortius, a Gyorsabban, magasabban, erősebben szelleme is tükröz. Másodpercek, méterek, álomhatárok, érmek, pontverseny, és a versenyzők számának függvényében utazó szakemberek népes gárdája – mintha mindenki a számok bűvöletében élne. De ugyanennek a bűvöletnek a részese a piaci verseny, a gyártók fejlesztési stratégiája, az űr-, Hold- Marsutazások prognosztizálása, az egy főre eső GDP varázsigéje, a digitális technika vagy a lélekszámot figyelembe nem vevő fiktív, virtuális hatalmi rendszerek tévképzetei, amik lassan-lassan megértek a változásra.
Mintha a számosság, a számszerűség, egyedül az anyagiság mércéje volna, a mérhetőség, a fizikai dimenziók szinte egyedüli kifejezője. Mondják egyesek, ami nem mérhető, az nincs is. A számoktól remélünk pontosságot, a precizitást, a matematikától egzaktságot, a tömegességtől biztonságot, a bináris kódokra bontástól jól kezelhetőséget. Az „egy élet, egy haza, egy Isten” az úgynevezett azonosítási paradigma viszonylag könnyen követhető egyenlete volt, ma azonban felülpecsételt vonalkód, kozmopolita szellem és az Isten likvidálása jellemzi a közállapotokat.
Jóllehet a matematikai készség sok esetben együtt jár a zenei érzékkel, s például Bartók zenéje az aranymetszés valóságos algoritmusa, a számokat mégis inkább a nyers és kimért realitás eszközeinek tekintjük, mint valamiféle művészetnek. Még kevésbé mitikus vagy misztikus eszköznek, pedig az archaikus kultúrákban a számoknak is megvolt a maga misztériuma, csakúgy, mint az írásjegyeknek, a szavaknak, vagy a hangoknak.
Mi maradt mára a számok misztériumából? Hol van az egzaktságon túl a művészet, a mindenség titkait sejtető játék? Hol, miben rejlik a számok titka, milyen mércét adnak a számok az ember kezébe a mindenség harmóniájának felméréséhez? Visszaadható-e még a XXI. században a számok ős-ereje, a mindenséget meghatározó és egyben visszatükröző misztériuma?
A számokat evidensnek tekintjük: egy, kettő, három, vagy még inkább 1, 2, 3… Bizonyos számok a szokásosnál is evidensebbek: a kéz ujjai szerint az öt, illetve a tíz, a hold mozgása szerint a 4×7=28, a kozmikus aránylátással bírók számára a 108, de erről majd később.
A számok olyannyira evidensek, hogy bár nap, mint nap használjuk őket, nem is észleljük, hogy az egy, a kettő vagy a zérus meghatározása milyen hihetetlen kihívás a tudomány számára. Ráadásul az egy egészen más, mint egy alma, az elvonatkoztatás nélkülözhetetlen.
A matematika írásbeli érettségi után legszívesebben minden magasabb műveletről megfeledkezünk, s csak a bankszámlánkon szeretjük látni az egyre több nullát tartalmazó számsorokat. Holott a számoknak az ilyen gyakorlati jelentésen túl sok kultúra mögöttes tartalmat is tulajdonít. Az archaikus korok tudására – jelen esetben a matematikával és a földméréssel szorosan összefüggő számmisztikára – a legtöbb esetben csak legyintünk: primitív korok primitív eszméi, féltudomány, megmosolyogni való tévtan. Ám amint szorult helyzetbe kerül az ember, könnyen folyamodik olyan eszközökhöz a segítség érdekében, amik addig nem is jutottak eszébe, vagy amiket egyenesen elvetett.
Számmisztika, kínai jós-számok, születési szám kalkuláció, numerológia, számséma alapján történő kártyavetés, kabbalisztika, nyereményjátékok nyerési esélyeinek számszerűsítése, babonás szám és mágikus számok – mind olyasmi, ami szöges ellentétnek tűnik például a matematika egzaktságához, a számszerű törvények kérlelhetetlenségéhez képest. Úgy mondják a számkultusz az idealista korok sajátja, a számok háttérbe szorulása pedig a realista idők sajátsága.
Az ókor s talán a világmindenség legismertebb misztikus matematikusa, Püthagorasz a számokban a mindenség alapvető építőköveit látta. Párhuzamot vont a számok, a zenei hangok, a morál és a kozmosz harmóniája közt, igazi holisztikus szemléletet képviselve elit-iskolájában, ahol az ifjúság színe-javát oktatta. Püthagorasz a párosságot tekintette a határozottság jelének, a páratlanságot pedig a határozatlanság jelének, s ennek alapján tíz alapelvet azonosított: 1. véges – végtelen; 2. páratlan – páros; 3. egység – sokaság; 4. jobb – bal; 5. hím – nő; 6. nyugvó – mozgó; 7. egyenes – görbe; 8. világosság – sötétség; 9. jó – rossz; 10. négyzet – oblongum.
Az iskola számára a számokkal való foglalatosság valóságos kultikus hit, egyfajta matematikai vallás volt, ami érdekes módon tér vissza a XX. században. Paul Dirac, a kor egyik kiemelkedő fizikusa így ír: „Valóságos hitkérdésnek tekintettük, hogy a természet alapvető törvényeit leíró egyenletekben nagy matematikai szépségnek kell rejtőzni. Ha tetszik, ez volt a vallásunk…”
Püthagorasz számára az „egy” a számosság ellentéte, egyben az isteni lényeg, a végső valóság megtestesítője, valójában nem is szám. Egynél kisebb szám nincs – mondották, s ez megfelel az archaikus világkép teljesség- igényének – nagyobb számok pedig ennek meg sokszorozásából keletkeznek. A két egyenlő részre osztható páros számok női jellegűek, s a kettő az első női szám, a két egyenlő részre nem osztható számok a hím természetűek, az első férfi szám a három. Az egy – ismét az archaikus szemlélet integritása szellemében – hímnős, sem nem maszkulin, sem nem feminin, nem páros, de nem is páratlan, hanem az eredet! A kettő és három összege az öt a házasság jelképe. A négy az első négyzetszám, ez az évszakok száma, igazság jelképe, s ezzel el is jutottunk az püthagoreusok első misztikus szintéziséhez, az első négy szám összegéhez: 1+2+3+4=10. A tíz már magasabb minőséget fejez ki, ez a természet harmóniájának, a tökéletességnek is száma. Hajdanán kavicsokkal számoltak, s ha a fenti számokat jelölő kavicsokat kirakjuk, eljutunk a püthagoreusok misztikus számkombinációjához, a szent tetraktüszhöz.
Mindannyian ismerjük a mágikus számnégyzeteket, melyeknél egy négyzethálón helyezkednek el a számok, s ahol a sorok és oszlopok, valamint az átlók mentén összeadott számok összege mindig ugyanannyi. A mágikus kozmológiában a bűvös négyzeteket hozzárendelik az egyes bolygókhoz – ez az adott bolygó kámeája –, ami tán visszavezethető a Püthagoreusok szent tetraktüszára, illetve „négyzetszámaira”.
A mágikus számnégyzetek jelentős szerepet kaptak az idevágó középkori szertartáskönyvekben, mert a négyzetet tartják a varázserő elsődleges forrásának. Ezeknek a számhálóknak távol-keleti rokonai is ismeretesek. A Kung Fu-Ce által elbeszélt legenda szerint a töprengő Jü császár előtt megjelent egy isteni teknőc, a páncélján egy sajátságos lenyomattal, a Lo-su ábrával. A nagyobb megbecsülésnek örvendő páratlan, fehér körök egyenesek mentén helyezkednek el, ezek képviselik a férfias jang jelleget, míg az alakzatba rendeződő fekete körök párosak és a nőies jin minőséget képviselik. Ha az alakzatok értékeit számokkal írjuk át, máris előttünk áll a talán legősibb, legalább háromezer esztendős bűvös négyzet.
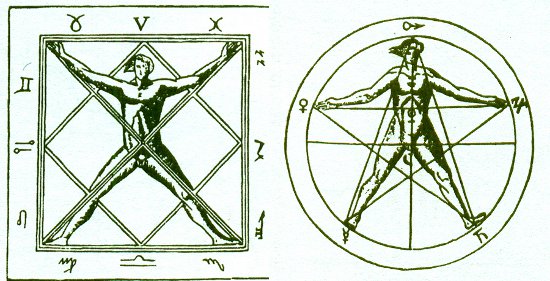
Ennek az ősi teknőcpáncélnak a fejtörőként ismeretes rokona a sudoku, amelyből egy könnyű és egy közepesen nehéz variáció található a cikk végén. A feladat az, hogy a 3×3-as kisebb négyzethálókba úgy írjuk be a számokat egytől kilencig, hogy azok a teljes ábra soraiban és oszlopaiban is csak egyszer-egyszer szerepeljenek. A játéknak csak egy lehetséges megoldása létezik! De nemcsak a valóban titokzatos számnégyzeteknek tulajdonítottak varázserőt, hanem az egyes számoknak is. Püthagorasz a keleti elődöket – kaldeus bölcseket és egyiptomi paptudósokat – követte, az ő nyomában pedig az évszázadokon keresztül tevékeny és eleven gnosztikusok jártak, akik biblikus alapon keresték a nevek, számok misztikus összefüggéseit. A varázslók mára gyermekivé enyhült igéje – abrakadabra – egyesek szerint a gnosztikus Abraxas istenségre vezethető vissza, akit leginkább a zoroaszter-hit időistenével, Zurvannal társítanak, de a görög Aiónnal és az indus tengeristennel, Varunával is kapcsolatba hozzák. Görög betűkkel kiírt neve a megfelelő számértékek alapján 365-öt tesz ki, így az esztendővel s a napjárással is összefügghet. A gnosztikusok számmisztikai tanait javarészt az ellenük íródott cáfolatokból ismertük, míg 1945-ben föl nem fedezték a Nag Hammad-i könyvtárat. A Jelenések könyvéből elhíresült szám a 666, a gonosz fenevad apokaliptikus száma. A betűkhöz rendelhető számértékek alapján kombinatorikai műveletek révén a latinus görög betűs átírása éppúgy ezt a számot adja ki, mint a romanus héber betűkkel írva. Talán a zsidóság a fenevadat a latinokban, a római birodalomban látta?! Néró császár nevének héber átírása szintén 666-ot tesz ki, sőt, némi csűrés-csavarással a pápai titulusból (Vicarius Filii Dei – Isten fiának helytartója) is kiolvasható az apokaliptikus szám. A Jelenések könyve amúgy is a számmisztika, a számosság egyik fő forrása a Bibliában (hét pecsét, hét angyal, Alfa és Ómega, hét csillag, csupaszem szárnyas négy élőlény, 24 vén, 12 csillagos korona a napba öltözött asszonyon, hétfejű sárkány, 12 kapus város stb.) Az Ószövetség negyedik könyve a Számok könyve (Numeri), ami egy korabeli népszámlálásról számol be, általában túlságosan magas értékekkel, ami sok egyéb adattal ellentmondásban van. Sajátságos számfejtés eredménye a 801, ami az üdvözítő nevének görög betűs átirata számértékeiből adódik, a 99, ami az ámen szám-olvasata, a 643 a szentháromság száma, a 999 a tökéletességé, továbbá a kabbalisztikus hagyományban gyakori 59, 49, 37, 24, valamint a pentagramm vagy boszorkányszög, az ötágú csillag misztikus száma, a 36. Ezzel függ össze a platóni bűvös szám, a 216, ami nem más, mint 63 vagy 5 × 36 + 36 vagy 13 × 23 × 33 vagy (1×2×3) × ( 12 × 22 × 32).
Az ősmagyar hitvilágban szentnek tekintették a hetes számot, a kínaiak az ötöst, az indogermánok pedig a kilencest. Ezek az emberhez legközelebb álló okokkal: a kéz öt ujja, a holdnegyedek hét napja, az embrió kilenc hónapos fejlődése magyarázhatók. A különböző kultúrákban a legnevezetesebb kitüntetett, szent vagy babonás számok a 3, 7, 9, 12, 13, 50, 66, 70, 77, hetedhét, 99, 100, 300, 600, 900.
S hogy mi volt előbb, a számolás vagy az írás? Nehéz volna eldönteni, hiszen az Afrikában, Mezopotámiában vagy Kínában föllelt első írásjelek lehetnek számok, de mértékegységek is, mindenesetre az egy bölény különbözik az „egy” absztrakt fogalmától, így bizonyosra vehető, hogy a számok és különösen a matematika magasabb kulturális vívmánynak tekinthető.
Az archaikus világképben a beszéd és annak rögzítése az írás, valamint a számok és az aritmetika szorosan összefügg és a mindenség benső harmóniáját tükrözi. Erre utal az is, hogy gyakorlatilag az összes ókori kultúra írásbeliségéhez számszerűséget is hozzárendeltek, úgy a zsidók, mint a görögök, az egyiptomiak vagy a hinduk.
A szavak, illetve hangok számértékét Indiában a matematika sajátságos kódjaként is használták, ötvözve a művészi igényt a vallási mítosszal és a tudományos hatékonysággal. Versek, strófák memorizálása sokkal könnyebb, mint egy sok tizedesjegyű szám megjegyzése, s ha az ember ismeri a hangok számértékét, könnyen visszaidézheti a kívánt számot. A magánhangzók nem számítanak, csak a mássalhangzóknak tulajdonítottak számértéket, így a szerző minden lépésnél szabadon választhatta meg a magán- és mássalhangzókat. A gazdag variabilitás révén sajátos jelentésekkel egészíthette ki mondandóját. A kapa, tapa, papa vagy japa kifejezések számértéke egyaránt tizenegy. A magán- és mássalhangzók sajátos megválasztásával akár kettős vagy hármas jelentésű költői himnuszok is fogalmazhatók. Vegyünk például egy lelki töltésű szútrát, ami ugyanakkor matematikailag is értelmezhető.
gópi bhagja madhuvrata szrngisó dadhi shandhiga khala dzsívita khatáva gala hálá raszandhara
Ez a vers egy Krsnához intézett fohász, egyúttal a π tizedrészének (vagyis a kör kerületének az átmérőjéhez aránya, osztva tízzel) harminckét helyiértékig pontos definíciója. Emellett egy olyan kulcs is benne foglaltatik, amely korlátlan számú helyiértékig pontos definíciót jelent.
A szútra fordítása a következő: „Óh, pásztorlánykák imádatának joghurtjával felkent Uram! Óh, elesettek megmentője, óh, Siva mestere, kérlek, oltalmazz engem!” A fenti mássalhangzó-kód segítségével a vers jelentése tizedes törtként értelmezve a értékének tizedét adja: /10 = 0.3141592653589793238462643 3832792. Így egyszerre hódolhat az ember odaadással Istennek, ugyanakkor fontos evilági adatokat is könnyedén megjegyezhet.
Az algebra kifejezés az ismeretlen mennyiségek számokkal történő behelyettesítésére, illetve az így folytatott számolásra vonatkozik, s az arab al-gebr szóból ered ( gabar jelentése: visszaállít). Itt jegyezzük meg, hogy az al-chemia nem nyert olyan tudományos elismertséget, mint matematikus testvérei, az al-gebra vagy az al-goritmus. E kifejezések Abdallah Mohammed ben Musa Al-Hvarizmi arab matematikus 820-ban megjelent munkájában fordulnak elő először, de magának az algebrának a keletkezése az ókorra nyúlik vissza. Az első- és másodfokú egyenletek megoldását a hellén tudományosság is ismerte, de idővel megrekedt a görög matematika. A kutatók közt megoszlanak a vélemények, miszerint a helyiérték rendszer talán Mezopotámiából származik, mások a zérus keletkezését a taoizmus üresség- elméletével kötik össze, ám ha figyelembe vesszük az adottságok együttállását – a tízes alapú számrendszert, a helyiérték használatát és a zérus használatát – mégis úgy tűnik az indus matematikáé a pálma. Az Indiában használatos tízes helyiérték és a zérus azonban igen hathatósnak bizonyult, s a tudós bráhmanák magas fokra emelték az indiai matematikát. Ezt tükrözi az indiai számrendszer, amely már az ókorban is hihetetlen számértékeket kezelt könnyedén a tíz hatványaival.
A védikus matematika egyik legjelesebb képviselője Bharati Krsna Tirtha Mahárádzs, a Védikus Matematika című munkájában bepillantást enged az ősi ind számtan finomságaiba. Az Atharva-védát idézve számos olyan szútrát, kódot vagy aforizmát említ, amelyek gyakorlatilag a matematika összes ágára vonatkozhatnak, a számtanra, az algebrára, síkbeli és térbeli geometriára és trigonometriára, a geometriai és analitikus kúpszelettanra, a csillagászatra vagy a differenciál- és integrálszámításra, s így tovább. A szútrák segítségével rendkívül egyszerűen, fejben elvégezhetők olyan számítások, melyekhez az ún. modern módszerekkel hosszabb időre van szükség. Az 1/29-ed értékű szám tizedes törtté alakítása általában 28 lépésben oldható meg, ám az ősi indus módszer segítségével ehhez egyetlen lépés is elegendő. Indiában a Pitagorasz-tételt (kb. i.e. 540) egy építészeti Sulba-szútrában az i.e. nyolcadik századnál korábban jegyezték le. Az itt kialakult számjegyeknek és fejlett tudományosságnak a közvetítői az arabok voltak, rajtuk keresztül találkozott az európai tudományosság a keleti tudósok eredményeivel. Leonardo Fibonnacci, más néven Pisano olasz matematikus (1180-1250) Arábiában diplomáciai szolgálatot teljesítő atyja mellett tanult arab nyelvet és matematikát. Liber Abaci (1202) című művében vezette be Európába az indiai vagy „arab” számokat.
A számok olykor mágikus felhangok nélkül is varázslatosan működnek. Minden misztika nélkül szintén Püthagorasz ismerte föl a tökéletes számok és a baráti számpárok jelenségét. Tökéletes számnak nevezték azt a számot, amely egyenlő az önmagánál kisebb osztóinak az összegével. Ilyen például a 6, mert 1+2+3=6, ahol 1, 2 és 3 a 6 osztói. További tökéletes szám a 28, hiszen 1+2+4+7+14=28, valamint a 496 és a 8128. Eddig terjedt a püthagoreusok ismerete, s az ötödik tökéletes számot Regiomontanus (1436-1476) lelte meg – ez a 33 550 336. A XVI. században Scheybl német matematikus találta meg a hatodik és hetedik tökéletes számot az n=16 és n=18 kitevőkre, s a XIX. század további négy tökéletes számot hozott: 260(261-1), 288(289-1), a 2106(2107-1) és a 2126(2127-1). A XX. században számítógépekkel azonosították a további tökéletes számokat: 2520(2521-1), 2616(2617-1), 21278(21279-1), 22170(22171-1), 22202(2203-1), 22280(22281-1), 23216(23217-1) és a 244 496(244 497-1).
Hasonlóképpen izgalmas felismerése volt az ókori matematikusnak egy baráti számpár meglelése, amelyek bármelyike egyenlő a másik valódi osztóinak – az 1-et is beleértve – az összegével. Ilyen baráti számpárként ismerték a 220 és a 284 számpárt. A 220 osztóinak összege: 1+2+4+5+10+11+20 +33+44+55+110=284 és a 284 osztóinak összege 1+2+4+71+142=220. A IX. században egy arab matematikus, Szábit ibn Kurra (836-901) fedezte fel az 1184 és 1210 baráti számpárt, Pierre Fermat (1601-1665) francia tudósé a 17 296 és 18 416 páros felismerése, René Descartes (1596-1650) adta meg a 9 363 584 és 9 437 056 baráti számpárt, a kimagasló Euler pedig (1707-1783) további 61 baráti számpárt határozott meg!
Az alábbi számsorok és oszlopok csak első pillantásra tűnnek ijesztőnek, de már az elrendezés is sejtet valami szépséget, s ha alaposabban áttekintjük a táblákat, meglepő törvényszerűségek tűnnek elő.
1 x 8 + 1 = ……………………………..
12 x 8 + 2 = ……………………………..
123 x 8 + 3 = ……………………………..
1234 x 8 + 4 = ……………………………..
12345 x 8 + 5 = ……………………………..
123456 x 8 + 6 = ……………………………..
1234567 x 8 + 7 = ……………………………..
12345678 x 8 + 8 = ……………………………..
123456789 x 8 + 9 = ……………………………..
1 x 9 + 2 = ……………………………..
12 x 9 + 3 = ……………………………..
123 x 9 + 4 = ……………………………..
1234 x 9 + 5 = ……………………………..
12345 x 9 + 6 = ……………………………..
123456 x 9 + 7 = ……………………………..
1234567 x 9 + 8 = ……………………………..
12345678 x 9 + 9 = ……………………………..
123456789 x 9 +10= ……………………………..
9 x 9 + 7 = ……………………………..
98 x 9 + 6 = ……………………………..
987 x 9 + 5 = ……………………………..
9876 x 9 + 4 = ……………………………..
98765 x 9 + 3 = ……………………………..
987654 x 9 + 2 = ……………………………..
9876543 x 9 + 1 = ……………………………..
98765432 x 9 + 0 = ……………………………..
Az alábbi sorozat pedig a szimmetria valóságos gyöngyszeme:
1 x 1 = ……………………………..
11 x 11 = ……………………………..
111 x 111 = ……………………………..
1111 x 1111 = ……………………………..
11111 x 11111 = ……………………………..
111111 x 111111 = ……………………………..
1111111 x 1111111 = ……………………………..
11111111 x 11111111 = ……………………………..
111111111 x 111111111 = ……………………………..
E gyönyörű számolási példák után térjünk vissza a számokból levezetett következtetésekre. Sokan az emberélet számos aspektusát igyekeznek megérteni a csillagokból, a jelekből vagy éppen a számokból. Egy barátom mesélte, amikor ő éppen a számok bűvöletében élt, mindent ilyen szemmel nézett, s még lakása ajtajainak számában is misztikus jeleket vélt fölfedezni. Ennél higgadtabban érdemes körülnézni, számolni. Dan Millman rendszerére támaszkodva, ha születési dátumunk számait összeadjuk (amennyiben a XX. században jöttünk a világra), majd redukáljuk, olyan kódot kapunk, amely segíthet az életfeladat beazonosításában. Például: 1967. augusztus 12 összegzése az alábbi: 1+9+6+7+0+8+1+2 = 34 majd ez redukálva: 3+4 = 7. A 87. oldalon (lent) található táblázat ad tájékoztatást az életfeladat általános vonásairól, lehetőségeiről. A lehetőségek negatív előjellel veszélyekké válhatnak, éppen ezért a figyelmesség mindenképpen tanácsos, de a tiszta szívű belső önvizsgálat és meditáció segít az eligazodásban.
Erdei Levente
2008/48.